Методы решения задач синтеза оптимальных систем

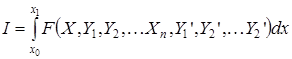(1.4.1.8)

Допустимая функция представляется в следующем виде

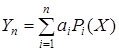(1.4.1.9)

где - постоянные коэффициенты, Pi - некоторые заданные функции. Подставив его в уравнение для (1.4.1.9), получим функцию коэффициентов ai

.

Далее выбираем ai так, чтобы минимизировать I. Решая, например, систему уравнений вида

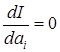(i =1, 2, …, n)

при , получаем функцию, которая при которая при некоторых дополнительных ограничениях является решением вариационной задачи.

При применении описанных выше методов к решению задач теории оптимальных систем необходимо иметь в виду следующие особенности задач теории оптимальных систем по сравнению с классическими вариационными задачами.

а) В выражение минимизируемого функционала в условия ограничений входят не только координаты объекта X, но и управляющие воздействия Uj(j=1, 2, , r).

б) Ограничения имеют обычно форму неравенств. Причем вектор может находиться не только внутри, но и на границах допустимой области F().

в) Решением оптимальной задачи часто являются кусочно-непрерывные функции Uj(t) с конечным числом точек разрыва первого рода, причем заранее не известно, когда происходят скачки Uj.

Обсуждая указанные особенности, заметим, что первая особенность сама по себе не вызывает затруднений. Нужно только включить Uj в качестве функции, рассматриваемой наравне с Хi. В данном случае вместо n-мерного фазового пространства нужно рассматривать (n+r)-мерное пространство с координатами X1, ., Хn, U1, ., Ur. Вторая особенность связана уже с большими затруднениями. Ограничения в виде неравенств можно в некоторых случаях свести к ограничениям в виде равенств, введя некоторую другую функцию. Однако это не всегда возможно и в некоторых случаях это может усложнить задачу. Требование того, чтобы Uj находилось и на границе допустимой области, может явиться в некоторых случаях причиной серьезных затруднений.

Что касается третьей особенности, то она усложняет выкладки и делает практически невозможным решение задач классическим путем, так как оптимальное управление U во многих случаях имеет разрывы первого рода [4].

В связи с указанными особенностями исключительную роль при решении задач оптимального управления играют возникшие в 50-х годах прошлого столетия неклассические методы решения вариационных задач-это принцип максимума и динамическое программирование.

.4.2 Принцип максимума

Академиком Л.С. Понтрягиным и его учениками в-1956 г. был предложен неклассический метод решения вариационных задач - принцип максимума.

Этот метод обоснован как необходимый и достаточный признак для линейных систем и необходимый для нелинейных систем. В дальнейшем была доказана справедливость принципа максимума для линейных дискретно-непрерывных систем и систем с распределенными параметрами [2].

Пусть система уравнений С-части (рис. 1. 4.2.1) имеет вид

, (1.4.2.1)

где Xi - координаты системы (i=1, …, n);

Uj - управляющие воздействия (j=1, …, r).

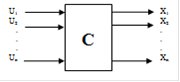
Рис. 1.4.2.1. Структурная схема системы дифференциальных уравнений.

На управляющие воздействия Uj, в R-мерном пространстве наложены ограничения , где v - дозволенная область управлений.

Введем вспомогательный вектор-функцию , координаты которого , заданы такой системой уравнений

; (i=1,…,n). (1. 4.2.2)

Систему уравнений (1.4.2.2) для называют сопряженной системой.

Образуем функцию Н

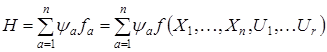(1.4.2.3)

Используя функцию Н, можно уравнения (1.4.2.1) и (1.4.2.2) записать в виде уравнений Гамильтона

(1.4.2.4.)