Методы решения задач синтеза оптимальных систем

Принцип максимума можно использовать для расчета оптимальной траектории. Допустим, что мы задались произвольным значением , (t = 0). Для малого промежутка времени ∆t, задавшись Uj, можно найти значения Хi и , в конце интервала. Варьируя Uj, на интервале ∆t, можно добиться того, чтобы значение H на этом интервале было максимальным. Таким образом, мы можем получить малый участок оптимальной траектории ∆Xi определить координаты его конца (Xi)t=0 + ∆Xi, а также значение вспомогательной функции в конце интервала ∆t.

Повторяя указанную операцию для следующего шага ∆t, можно найти следующую точку оптимальной траектории и в конечном счете получить всю оптимальную траекторию Ri. Оптимальная траектория будет найдена тем точнее, чем меньше берется величина интервала ∆t. Естественно, что чем меньше брать ∆t, тем больший объем вычислительной работы необходимо проделать для нахождения оптимальной траектории.

Следует указать, что при определении оптимальной траектории задаемся произвольными начальными значениями.

Подбор требуемого значения . Для траектории R* можно автоматизировать, если для каждой траектории измерять, например, минимальное расстояние до точки О или величину

.

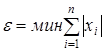Автоматическая система в этом случае должна будет так подбирать чтобы минимизировать . Таким образом, при непосредственном использовании принципа максимума для нахождения оптимальной траектории необходима двойная оптимизация: максимизация H на каждом интервале ∆t и минимизация для траекторий Ri.

Вычисление оптимальной траектории этим методом может производиться на модели ручным способом или автоматически, варьируя управляющими воздействиями Uj и начальным значением функции .

Метод динамического программирования

В основе метода динамического программирования лежит принцип оптимальности, сформулированный Беллманом, содержание которого сводится к следующему: если траектория системы оптимальна на отрезке времени [0, T] то конечный участок этой траектории на отрезке [t’, T] в свою очередь является оптимальной траекторией, где t’(0<t’<T) - произвольный момент времени [2]. Поясним это положение. Пусть на траектории функционал

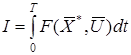(1.4.3.1)

принимает минимальное значение, и пусть взят некоторый момент времени t’(0<t’<T)). Тогда для траектории на отрезке времени [t’, T] функционал

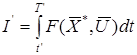
будет также минимален.

Для доказательства предположим противное, то ecть, что существует для отрезка [t’, Т] траектория , отличная от и дающая наименьшее значение функции налу. Но это бы означало, что траектория, состоящий из для t на промежутке [0, t'] и на отрезке [t',T], давала бы функционалу I значение, меньшее на отрезке [0, Т], чем , а это противоречит условию, что - оптимальная траектория. Это противоречие и доказывает справедливость принципа оптимальности.

Несмотря на простоту формулировки и кажущуюся примитивность, принцип оптимальности позволил построить весьма мощный метод решения вариационных задач. Глубокий смысл принципа оптимальности можно уяснить, если сравнить его с таким утверждением, которое кажется весьма очевидным: «если траектория оптимальна, то и каждый участок ее оптимален». Однако это утверждение не всегда верно. Убедимся в этом на примере. Пусть бегун бежит на длинную дистанцию. Его цель, выбирая на каждом участке определенную скорость, минимизировать время прохождении дистанции в целом, то есть функционалом является время 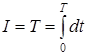(здесь ). Но минимизирует ли при этом бегун I на каждом участке. Иначе говоря, проходит ли он каждый отрезок пути с максимальной скоростью. Нет, конечно. Если он будет так бежать, то быстро выдохнется.