Методы решения задач синтеза оптимальных систем

Принцип оптимальности будет выполняться, если, не думая и им, как пройден начальный участок пути, в каждый момент времени бегун будет строить свое поведение так, чтобы оставшийся путь пройти за минимальное время, оценивая, пополню, свое состояние в этот момент.

Указанный пример помогает понять другую формулировку принципа оптимальности:

Оптимальная стратегия определяется лишь состоянием системы в настоящий момент и не зависит от того, как система пришла в данную точку.

Рассмотрим метод динамического программирования на примере [3].

С помощью метода динамического программирования решим задачу об оптимальном быстродействии.

Пусть объект описывается линейным дифференциальным уравнением

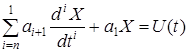(1.4.3.2)

Обозначим

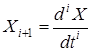; ; …; ; …(i =1, 2…n-1).

Представим (1.4.2) в виде системы n-уравнений первого порядка

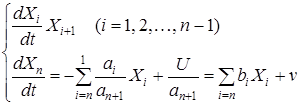(1.4.3.3)

где: ; .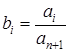

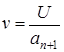Пусть на v наложено ограничение вида

. (1.4.3.4)

Необходимо найти оптимальное управление v(t), обеспечивающее минимальное время Т перемещения изображающей точки из начального положения Х1(0), . . ., Хn(0) (радиус-вектор ) в начало координат фазового пространства.

Если положить в (1.4.3) Т = N∆t, Xi(К) = Xi(К∆t), v(К) = v(К∆t), то уравнение (1.4.3.3) запишется в конечных разностях

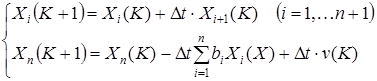(1.4.3.5)

Рассмотрим минимальное время попадания в некоторую коночную точку с координатами

(i =1,2. , N). (1.4.3.6)

Минимальное время Т попадания в эту точку зависит лишь от начальных условий X1(0), X2(0), . . ., Хп (0), то есть Т= Т[(0)]. Переход из начального положения на один шаг занимает время , после чего вектор (0) будет заменен вектором (l), который зависит от v(0). Минимальное время попадания из точки (1) в точку (N) будет функцией только от (1): Т=Т[(1)], а общее время равно, что можно записать так

. (1.4.3.7)

Если в уравнении (1.4.3.7) (1) записать согласно (1.4.3.4), то получим

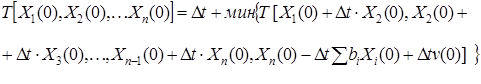(1.4.3.8)

Если принять, что Т - дифференцируемая функция переменных Xi(0), то, раскладывая второе слагаемое в правой части (1.4.3.8) в ряд по степеням Xi(0) и отбрасывая слагаемые выше первого порядка, уравнение (1.4.3.8) можно записать так

(1.4.3.9)

,

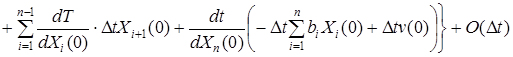где - остаточный член, порядок малости которого выше . В уравнении (1.4.9) от v(0), по которому идет минимизация, зависит только последнее слагаемое в фигурной скобке, поэтому знак минимизации можно отнести только к этому члену, при этом T[X1(0), . . ., Хп(0)] и обеих частях уравнения взаимно уничтожится. Разделим теперь уравнение (1.4.3.9) на и устремим к нулю, так как имеет более высокий порядок малости, чем . В результате получим