Методы решения задач синтеза оптимальных систем

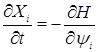. (1.4.2.5)

Так как fi- координаты вектора в фазовом пространстве, а -координаты вектора уравнение (1.4.2.3) можно записать в виде скалярного произведения

. (1.4.2.6)

Сформулируем принцип максимума.

Для получения оптимального процесса, нужно в любой момент времени выбирать такие Uj, чтобы величина Н была максимальна.

Дадим геометрическую интерпретацию принципу максимума.

Установлено, что вектор есть ни что иное, как нормаль к поверхности S изохроны, соответствующей минимальному времени перехода из точки в заданную точку фазового пространства (в полюс изохроны). Связь между и S() такая

или . (1.4.2.7)

Как видно совпадает с направлением наибыстрейшего уменьшения S, то есть уменьшения оптимального времени переходного процесса. Условие Н = макс совпадает с условием максимизации скалярного произведения и . Но так как вектор в данной точке задан и не зависит от , то условие Н= макс соответствует максимуму проекции вектора на направление .

Следовательно, геометрический смысл принципа максимума заключается в следующем: необходимо подбирать такое управление , чтобы проекция вектора скорости на направление нормали к изохроне в данной точке была максимальна.

Рассмотрим частный случай, когда явная зависимость от времени t в уравнении движения отсутствует и требуется обеспечить минимальное время переходного процесса Т. В этом случае принцип максимума принимает форму

(1.4.2.8)

Траектория изображающей точки в n-мерном пространстве (рис.1.4.2.2) должна быть оптимальной. Для этого следует подбирать оптимальное управление так, чтобы в каждый момент времени максимизировать Н, причем максимальное значение в любой точке траектории равно 1.

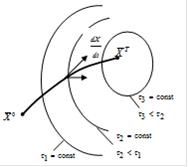
Рис. 1.4.2.2 Траектория изображающей точки в n-мерном пространстве

В данном случае

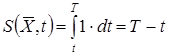
где: t - текущий момент времени.

Таким образом, время достижения конечной точки уменьшается по мере увеличения t, а вектор , совпадающий с наискорейшим уменьшением S, обращен внутрь изохрон t = Т - t,t охватывающих конечную точку . Принцип максимума здесь означает такой подбор , чтобы проекция скорости изображающем точки в фазовом пространстве на направление нормали к изохроне была максимальна. Это легко доказывается из следующего очевидного положения: движение по изохронам не уменьшает времени достижения точки . Между тем, чем ближе происходит движение к нормали к изохроне, тем скорее изображающая точка достигнем конечной точки [4].